WebGL笔记（二）变换

变换包括平移、旋转、缩放等，单纯地用数学表达式可以实现变换功能，但遇到复杂的变换，数学表达是就有些吃力了，这时候变换矩阵就派上了用场；下面用这两种方式分析一下变换的基本原理；

一、数学表达式

查看平移、旋转、缩放的demo请点击这里；

1、平移

顶点着色器代码

attribute vec4 a_Position;
uniform vec4 u_Transition;
void main(){
  gl_Position = a_Position + u_Transition;
  gl_PointSize = 10.0;
}

上面的代码表示以 a_Position 坐标为基准，移动 u_Transition 这个向量，a_Position 和 u_Transition 都是 vec4 类型的，可以直接相加；

vec4 类型中，最后一个分量 w 是齐次坐标，平移情况下，两者相加只能为1，否则就把图形放大或缩小了；

2、旋转

描述旋转有3个属性：旋转轴、旋转方向、旋转角度；

逆时针旋转也可以称作正旋转，可以用右手法则来确定，右手握拳，大拇指伸直并使其指向旋转轴的方向，其余手指的方向就是逆时针；

将二维坐标系中的一个点(x, y)沿原点旋转角度β，则旋转后的坐标(x1, y1)为：

x1 = x*cosβ – y*sinβ
y1 = x*sinβ + y*cosβ

这两个公式直接作为结论记住就可以了，推导的话，在坐标系中实际操作一下，画两个直角三角形就可以；

由上面的公式可以编写顶点着色器代码：

attribute vec4 a_Position;
uniform float u_SinB, u_CosB;

void main(){
  gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;
  gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;
  gl_Position.z = a_Position.z;
  gl_Position.w = a_Position.w;
  gl_PointSize = 10.0;
}

公式中的 sinβ、cosβ 在js中计算好了传进来

var angle = 80;
var u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');
var u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');
var rad = 2 * Math.PI * angle / 360; // 角度转弧度
gl.uniform1f(u_SinB, Math.sin(rad));
gl.uniform1f(u_CosB, Math.cos(rad));

js 中的 Math.cos()、Math.sin() 参数为弧度，角度转弧度：一周 2π=360°，按比例算一下就可以了；

上面是两个参数分开，也可以直接把两个值一块儿传过去，比如用 uniform2f 方法，传两个值 gl.uniform1f(u_SinCosB, Math.sin(rad), Math.cos(rad))；顶点着色器中，使用 u_SinCosB.x、u_SinCosB.y 来获取；

* 3、缩放

平移中提到了，可以用齐次坐标来控制缩放；

二、变换矩阵

1、矩阵和矢量相乘

上面的矩阵 [a…i] 乘 向量(x, y, z) 的公式为：

x’ = ax + by + cz;
y’ = dx + ey + fz;
z’ = gx + hy + iz;

不支持交换律，即 A×B 不等价于 B×A；

2、平移、旋转和缩放矩阵

原理

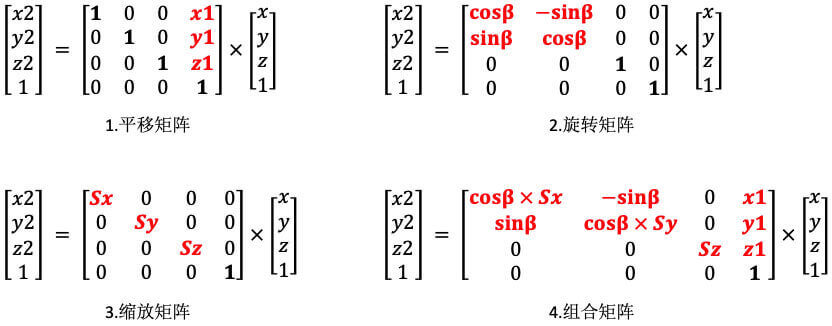
上面的矩阵中，(x, y, z, 1) 表示点的初始坐标；(x2, y2, z2, 1) 表示转换之后的新坐标；(x1, y1, z1) 表示平移的矢量；cosβ、sinβ表示β这个角度的余弦、正弦值；(Sx, Sy, Sz) 表示 x、y、z 三个方向的缩放倍数；

原始的4×4矩阵是一个主对角线值均为1的对角矩阵，其他操作都是在这个基础上替换值；

数学中的矩阵是按行存储的，WebGL/OpenGL 中的矩阵是按列存储的，专有名词为按行主序（row major order）和按列主序（column major order）；

具体代码

顶点着色器代码如下，直接用矩阵和位置向量相乘

attribute vec4 a_Position;
uniform mat4 u_Matrix;
void main(){
  gl_Position = u_Matrix * a_Position;
  gl_PointSize = 1.0;
}

js 中的相关操作代码如下：

// 设置矩阵
var trans = {x: 0, y: 0, z: 0, w: 1.0};
var scale = {x: 1.2, y: 2, z: 1};
var angle = 0;
var rad = 2 * Math.PI * angle / 360; // 角度转弧度
var sinB = Math.sin(rad), cosB = Math.cos(rad);

var matrix = new Float32Array([
  cosB * scale.x, sinB, 0.0, 0.0,
  -sinB, cosB * scale.y, 0.0, 0.0,
  0.0, 0.0, scale.z, 0.0,
  trans.x, trans.y, trans.z, trans.w,
]);
// 传递参数
gl.uniformMatrix4fv(u_Matrix, false, matrix);

这段代码中，有一个需要注意的地方，trans 平移向量的最后一个分量为1.0，因为这里是相乘；在数学表达式方式中，这个分量是0，因为是执行相加操作；

gl.uniformMatrix4fv(u_Matrix, false, matrix)

该操作的含义：用 matrix 表示的 4×4 矩阵分配给 u_Matrix 这个 uniform 变量；

第二个参数表示是否转置矩阵，转置操作会交换行和列，但WebGL没有实现矩阵转置的方法，这里必须设置为false；

uniformMatrix4fv 中的 v 表示可以向着色器传输多个数据值；

如果第二个参数设置为true，或者第三个参数 matrix 的数组长度不是16，Chrome 中会报 Warning，而不是 Error；

源代码在这儿

三、高级变换和动画

1、复合变换

对原始坐标进行多个变换时，实际的矩阵操作是按照逆序进行的；

比如对一个三角形依次进行平移、旋转、缩放，具体的代码中，矩阵操作要先缩放，再旋转，最后在平移；推导过程如下：

平移后的坐标 = 平移矩阵 × 原始坐标；

旋转后的坐标 = 旋转矩阵 × 平移后的坐标
= 旋转矩阵 × ( 平移矩阵 × 原始坐标 )

缩放后的坐标 = 缩放矩阵 × 旋转后的坐标
= 缩放矩阵 × ( 旋转矩阵 × ( 平移矩阵 × 原始坐标 ) )

最后一个公式中，括号可以去掉，矩阵乘法不支持交换律，但支持结合律，把原始坐标摘出来，对应到顶点着色器中的代码“变换矩阵 × 原始坐标”，则整理后的公式：

变换后的坐标 = ( 缩放矩阵 × 旋转矩阵 × 平移矩阵 ) × 原始坐标

2、作者整理的矩阵操作库

作者整理了一个矩阵操作的库，源代码在 coun-matrix.js 中，还是有点用的；

* 官方examples在这儿，翻不了墙的可以在github这里找到，但都不是原作者创建的；

该库中有一个 Matrix4 类/函数，使用时先要 new 一个对象 var mat4 = new Matrix4()，然后就可以使用下面这些支持的方法或属性了：

• mat4.setIdentity()：将当前实例初始化为单位矩阵（即上面提到的未经过变换对角线上值为1的原始对角矩阵）；
• mat4.setTranslate(x, y, z)：将当前实例的矩阵设置为平移矩阵；
• mat4.setRotate(angle, x, y, z)：将当前实例的矩阵设置为旋转矩阵，(x, y, z) 为旋转轴；
• mat4.setScale(x, y, z)：将当前实例的矩阵设置为缩放矩阵；
• mat4.translate(x, y, z)：当前实例的矩阵乘以一个位移为(x, y, z)的平移矩阵，计算结果会覆盖当前实例的矩阵；
• mat4.rotate(angle, x, y, z)：当前实例的矩阵乘以一个角度为angle，旋转轴为(x, y, z)的旋转矩阵，计算结果会覆盖当前实例的矩阵；
• mat4.scale(x, y, z)：当前实例的矩阵乘以一个缩放为(x, y, z)的缩放矩阵，计算结果会覆盖当前实例的矩阵；
• mat4.set(m)：将当前 Matrix4 实例替换成 m，m必须也是一个 Matrix4 变量；
• mat4.elements：当前实例的表示矩阵的类型化数组（Float32Array）；

3、动画

动画感觉没什么可说的，基本原理就是每隔多少时间绘制一次，每次绘制的内容比上次多一点，最终把所有内容绘制出来，动画结束；

下面是之前整理过的一篇动画分析，有兴趣的可以去看一下；

Canvas 动画分析

TODO

坐标系中，z轴是垂直于屏幕的，x轴正方向为屏幕右侧，y轴正方向为屏幕上侧；

上面的例子中，旋转的时候，三角形有形变，这就有问题了，原因可能有两个：1.三角形所在的面发生变化；2.计算公式有错误；

三点确定一个面，变化过程中，z坐标一直是0，也就是说，三个点应该是被固定在了xy轴组成的平面上，从这儿往后推，感觉公式有问题，但书出来这么多年了，有问题早就发现了；唯一合理的解释是旋转中心不在xy轴组成的平面上，但是书中也没有提到；

这个问题先保留，看后边的章节里有没有解释；