数据结构相关笔记
1、线性表
顺序存储
数组
链式存储
单链表:每个结点指向指向下一个结点;
双向链表:每个结点指向上一个和下一个结点,可以从两个方向上遍历链表;
循环链表:在单链表或双向链表的基础上,首尾相连,可以从任意结点遍历整个链表;
静态链表:数组;
栈和队列
栈:先进后出;
队列:先进先出;
两者都有两种存储结构:顺序存储、链式存储;
串
仅有字符构成的有限序列;– 字符串;
2、数组、矩阵和广义表
特殊矩阵:对称矩阵、三角矩阵、对角矩阵;
稀疏矩阵:在一个矩阵中,若非0元素的个数远远少于0元素的个数,且非0元素的分布没有规律;
广义表
广义表是线性表的推广,是由0个或多个单元素或子表组成的有限序列;
取表头:head(LS),第一个元素;
取表尾:tail(LS),除表头元素外的其他元素;
长度:广义表中元素的个数;深度:嵌套的层数;
3、树与二叉树
基本概念
- 树:n(n>=0)个结点的有限集合,n=0时为空树;在任一非空树中,有且仅有一个根结点,树结构是非线性结构;
- 双亲、孩子和兄弟:结点的子树的根称为该结点的孩子;相应地,该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟;
- 结点的度:一个结点的子树的个数记为该结点的度;
- 叶子结点:也称终端结点,指度为0的结点;
- 分支结点:也称非终端节点,指度不为0的结点;
- 内部结点:除根结点以外的分支结点称为内部结点,或除了根结点和叶子节点以外的结点;
- 结点的层次:根为第一层,根的孩子为第二层,以此类推,若某节点在第i层,则其孩子结点在第i+1层;
- 树的高度:一棵树的最大层数记为树的高度(或深度);
- 有序/无序树:若将树中各子树堪称是从左到右具有次序的,即不能交换,则称该树为有序树,否则称为无序树;
- 二叉树:每个结点最多有两个节点;
- 满二叉树:所有结点的度都是2;
- 完全二叉树:有右结点的时候,一定有左结点;有左结点,不一定有右结点;从左到右没有间断;
- 非完全二叉树:从左到右结点有间断;
二叉树遍历
前序遍历:按照 根-左-右 的顺序遍历;
中序遍历:按照 左-根-右 的顺序遍历;
后序遍历:按照 左-右-根 的顺序遍历;
层次遍历:从上到下,从左到右遍历;
* 什么序遍历,这个序指的是根的位置;
树转二叉树
左子树存放孩子结点;右子树存放兄弟结点;
查找二叉树
用二叉树对数据进行排序;
左结点的值小于根;右结点的值大于根;
删除时,如果一个结点P为叶子结点或只有一个子结点S,则直接删除结点P,后边的结点S补上即可;
删除时,如果一个结点P有两个子结点,则在左子树里用中序遍历查找值最大的结点S,用节点S替换P,然后删除节点S;
最优二叉树(哈夫曼树)
它是一类带权路径长度最短的树。路径是从树中一个结点到另一个结点之间的通路,路径上的分支数目称为路径长度;
- 树的路径长度是从根到每一个叶子之间的路径长度之和(长度相加);
- 结点的带权路径长度为从该结点到根之间的路径长度与该结点权值的乘积(长度*值);
假设有一组字符{a,b,c,d,e,f,g},对应权值为{8,21,3,11,9,5,14},请尝试构造哈夫曼树;
构造过程:
- 取权值最小的两个数相加,得到和,然后删除这两个数;3+5=>8,删除3、5,集合变为{8, 21, 11, 9, 14, 8}
- 重复1的过程,直到完成为止,将相加过程反应到数的结点上,就得到了下面的树;
- *实际中,权值应该是小于1的,为了方便计算和操作,设为了整数;
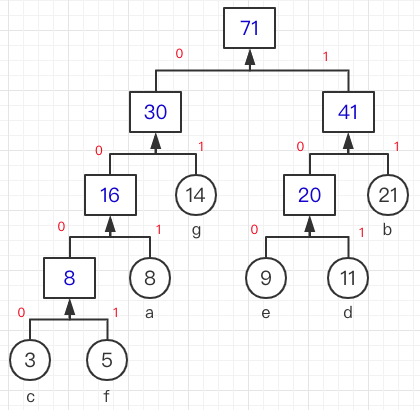
上面的树中,c 的编码是 0000,14 的编码为 01,权重越大(使用频率越高),编码长度越短,这种编码就叫做哈夫曼编码;
c 的带权路径长度为 4 * 3 = 12;
树的带权路径长度为:4*c + 4*f + 3*a + 3*e + 3*d + 2*g + 2*b = 186
树的路径长度为:4 + 4 + 3 + 3 + 3 + 2 + 2 = 21
线索二叉树
按照某些规则,让二叉树中的结点能够找到它的前驱和后继结点;
把二叉树这种非线性结构,转成线性结构;
前序、中序、后序线索二叉树;
比如一个结点对应的数字的前一个数字为它的父结点,后一个数字为整个树的右子树的第一个结点(前序);
平衡二叉树
任意结点的左右子树深度相差不超过1;
每个结点的平衡度只能为-1、0、1;
4、图
完全图
无向图:每对顶点之间都有一条边相连;
有向图:每对顶点之间都有两条有向边相互连接;
存储结构
邻接矩阵:xx
邻接链表:把每个顶点的邻接顶点用链表表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针;用来描述每个顶点能到达哪些顶点;
图的遍历
深度优先:从上往下,从左往右;
广度优先:从左往右,从上往下;
拓扑排序
AOV网络:有向图中,若以顶点表示活动,用有向边表示活动之间的优先关系,则称这样的有向图为以顶点表示活动的网;
图的最小生成树
对于连通网来说,边是带权值的,生成树的各边也是带权值的,因此把生成树各边的权值总和称为树的权;
把权最小的生成树称为最小生成树;即连通各个点需要最短的路径,它对应的生成树就是最小生成树(不一定是直接连接,只要有路到达即可);